Previous page     Contents     Next page

Among the phase transitions in clinopyroxenes described above, the P2₁/c to C2/c transition in kanoite MnMgSi₂O₆ clinopyroxene is of special interest because the transition temperature is much lower than in the (Mg,Fe,Ca)-clinopyroxenes, between 150 and 400°C depending on composition. This allows studies to be performed on the nature of the displacive phase transition without taking into account cation order-disorder phenomena. The phase transition involves stretching of the two independent silicate chains in the low-temperature (LT) phase until they become equal in the high-temperature (HT) phase.

The Raman experiments were perfomed on a DILOR XY triple spectrometer using the 514.5 nm line of Ar⁺ laser in an externally heated Bassett-type diamond-anvil cell (DAC). The sample temperature was measured with accuracy ±3°C. The spectra were decomposed using Lorentz profile functions and the DILOR LAB208 software.

The irreducible representations of the long-wavelength optical phonons were determined using the correlation method. In the LT phase 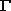_opt = 30A_g + 30B_g + 29A_u + 28B_u. In the HT phase 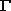_opt = 14A_g + 16B_g + 13A_u + 14B_u. In both phases the gerade(g) modes are Raman active while the ungerade(u) modes are IR active. The factor group analysis predicts that the phase transition leads to halving of the number of Raman active modes in the HT phase without change of the symmetry of the modes. The unpolarized Raman spectra in the range 100 - 700 cm^-1 measured at different temperatures are shown in Figure 3.2-1.

Fig. 3.2-1: Unpolarized Raman spectra of MnMgSi2O6 at different temperatures. The spectra are shifted along the y axis for clarity.

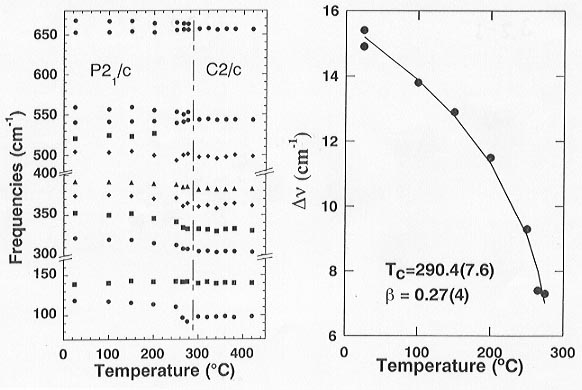
The assignment of the vibrational modes is based on lattice dynamics and Raman intensity calculations. In the LT phase the strong bands at about 1000 (not shown in Fig. 3.2-1), 660, 320 and 120 cm^-1 are A_g type modes. The B_g modes are generally much weaker. Different behavior of the Raman active modes as a function of temperature is observed (see Fig. 3.2-2).

Several modes at about 120, 320, 355 and 375 cm^-1 shift significantly below the phase transition temperature T_c ˜ 290°C to lower frequencies with increasing temperature, while the modes at about 140, 390, 510 cm^-1 exhibit only minor frequency changes. Evidently the former are strongly coupled, while the later are only weakly coupled to the order parameter Q. Several asymmetric bands at about 225, 660 and 1000 cm^-1 are observed.

The doublet structure of the 660 cm^-1 peak in the LT phase is most pronounced. The lattice dynamics calculations indicate that it consists of two closely spaced A_g modes which arise from symmetric bending motion of the bridging oxygens in the pyroxene chains. With increasing temperature these closely spaced A_g modes shift towards each other and merge into one broader A_g mode above T_c in agreement with the factor group analysis. The splitting of the A_g peaks at 660 cm^-1 below T_c provides a convenient measure of the temperature dependence of the order parameter. The splitting v is shown in Figure 3.2-3.

Fig. 3.2-2: Temperature dependence of the Raman frequencies.	Fig. 3.2-3: Frequency splitting of the Ag modes near 660 cm-1 as a function of temperature (·). The full line is a fit to the data using the expression v = A(Tc-T)ß.

The fitting of v to the expression v = A(T_c-T)^ß gives T_c = 290.4 ± 7.6°C and a critical exponent ß = 0.27 ± 0.04. The splitting is generally proportional in the lowest order to Q for the case of a first-order phase transition or to Q₂ in the case of second-order phase transition. Our results show that for kanoite the coupling of the A_g modes to the order parameter Q cannot properly be described by taking into account the lowest coupling terms only. We also do not see a real soft mode but additional measurements below 100 cm^-1 and detailed analysis of the temperature dependence of the Raman intensities and the full widths at half maximum will be necessary to understand fully the nature of the phase transition in kanoite.