Previous page     Contents     Next page

For the calculation of density contrasts between the phases involved in igneous petrogenesis, accurate pressure-volume-temperature (PVT) equations of state are required for all participating phases. For many solid solutions relevant to basaltic magmatism, adequate density models exist. Achieving the same state of progress for the multicomponent liquid phase participating in terrestrial and planetary magmatism remains a modern research goal. Recent work on the subject has been divided into two sorts of experimental investigations. The first relies on the high-temperature buoyancy-based methods derived from techniques in the glass and metallurgical sciences. Over the past fifteen years, high-temperature investigations of this type have given rise to refined multicomponent models of melt densities that have found widespread application in the Earth sciences. The high-temperature buoyancy-based methods provide direct density determinations over a restricted range of temperature. The temperature dependence of the density is fitted linearly to obtain expansivities of the investigated melts and multicomponent fits allow the derivation of high-temperature linear descriptions of the temperature dependencies of the partial molar volumes of oxide components. Such studies are undoubtedly useful in the high-temperature range for prediction of melt density. They do however suffer from the fact that the errors generated for the derived expansivity values can be very large. The use of expansivity data from such studies as input into further physico-chemical studies of silicate melts, such as ultrasonic investigations of wave velocities to obtain elastic constants, are seriously hampered by such errors. Additionally, the large errors contribute to a considerable uncertainty in extrapolating the density of the melts to significantly higher or lower temperatures.

In consideration of the above restrictions in the use of high-temperature, buoyancy-based density determinations, a new approach was introduced in the Earth sciences a decade ago. Dilatometric methods were applied to the determination of melt densities at low temperatures, just above the glass transition. This method involved the comparison of calorimetric and dilatometric traces of the temperature dependence of enthalpy and volume, respectively. It entailed an implicit assumption that the parameters controlling the relaxation of both enthalpy and volume were equivalent. This assumption passed all tests to which it could be put, including the equivalence of activation energies for both processes and the successful combined fitting of volume and expansivity data obtained using this method together with high-temperature, volume-temperature data from the traditional buoyancy methods described above. These dilatometric methods were subsequently employed in the development of a multicomponent model for granitic and pegmatitic melt volumes. One of the most striking and controversial results of the combined analysis of high and low-temperature density data was the proposal that the temperature-dependence of silicate melt densities is nonlinear, and that the expansivity decreases with temperature. This non-linearity in expansivity would invalidate, in detail, all pre-existing models for the calculation of melt density, which are based on linear volume-temperature relationships. Linear models, whether based on high-temperature data or low-temperature data could then no longer be used for extrapolation outside the temperature range of their calibration.

In this work, the expansivity of supercooled diopside liquid has been determined using techniques of container-based dilatometry (see 1998 Annual Report for methodological details). Two thermal strategies have been employed, one in which the sample is brought to volumetric equilibrium by long duration dwells at low temperatures (817°C) and one in which scanning dilatometry of the sample has been performed at somewhat higher temperatures (890-913°C). The results of both experiments yield a supercooled liquid expansivity for diopside liquid in the temperature range of 817-913°C of 84.4±2.8x 10^-4 cm³/mol K (Fig. 3.5-12). This expansivity is 65% higher than that obtained for diopside melt obtained at superliquidus temperatures using the double-bob Archimedean method.

Combined fitting of the new low-temperature, volume-temperature data from the present study and the superliquidus data from the literature has been performed. The fit of the combined data yields the following equations for the volume-temperature relationship of diopside liquid (T = temperature in °C):

The standard error of the fit using both equations reproduces the volume-temperature data for diopside liquid within experimental error. This result reconciles the disparate values of expansivity measured at low temperatures in the supercooled state and at superliquidus temperatures and confirms the non-linear temperature dependence of the expansivity of diopside liquid.

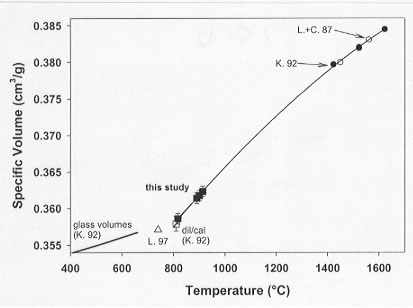Fig. 3.5-12: Diopside volumes from glass to superliquidus temperatures. High temperature buoyancy-based data by Knoche et al. (K. 92) and Lange and Carmichael (L.+C. 87) are in good agreement and reveal consistent stable liquid volumes. Comparison of supercooled liquid expansivities derived from container-based dilatometry with high-temperature expansivities indicates a non-linear volume-temperature relationship for diopside melts beyond the glass transition. The second-order polynomial fit to metastable and stable volumes reproduces the directly measured container-based volumes and expansivities excellently as well as the Archimedean-based high-temperature data.