Previous page     Contents     Next page

ELNES spectroscopy, being an analytical TEM technique, offers an ability to characterize materials on a nanometer scale (cf. section 3.4). In principle, one can obtain chemical and structural information for interfaces, defects, and nm-scale inclusions or particles. In practice however, acquiring, processing, and evaluating these spectra in a quantitative manner is neither trivial nor straightforward. In order to obtain optimal ELNES results, one must deal with the following acquisition and processing problems.

- High-energy electrons (200 keV) tend to amorphize crystalline materials in the electron microscope when the beam is focused to a small spot. Even within the short acquisition time required for parallel-detection ELNES (ca. 2 - 5 s), silicate minerals can be significantly damaged. This is particularly problematic for highly metastable high-pressure phases when acquiring Si K-edge spectra because a high electron flux is required to achieve adequate signal to noise ratios at the Si-K edge.

- Due to the energy spread of electrons from the Schottky-type field emitter of our microscope, energy resolution in our ELNES spectra is relatively low compared to XANES spectra (typically 0.8 to 1 eV, vs. 0.05 eV for XANES). This resolution approaches the linewidths of some of the component peaks in the near edge region, making it difficult to identify them distinctly.

- Obtaining spectra from thicker samples is often required to achieve good signal to noise ratios in materials where the concentration of the element of interest is low. Such spectra suffer from plural scattering of electrons resulting in increased background intensity at energies above the absorption edge.

In order to minimise these problems, we have, in addition to optimising microscope and detector parameters, developed the following aquisition and processing strategy:

1. For obtaining quality Si-K edge spectra from highly beam-sensitive materials such as wadeite-K₂Si₄O₉, samples are cooled to liquid nitrogen temperatures to slow amorphization so that acquisition times and signal-to-noise ratios can be increased.

2. For precise determinations of the positions, intensities, and half widths of component peaks (for comparison with theoretical multiple-scattering spectra) it is necessary to optimize the experimental resolution and then fit the spectra to theoretical line shapes. A Fourier-transform deconvolution of the spectra with the peak shape of the zero loss peak is used to sharpen edge features. 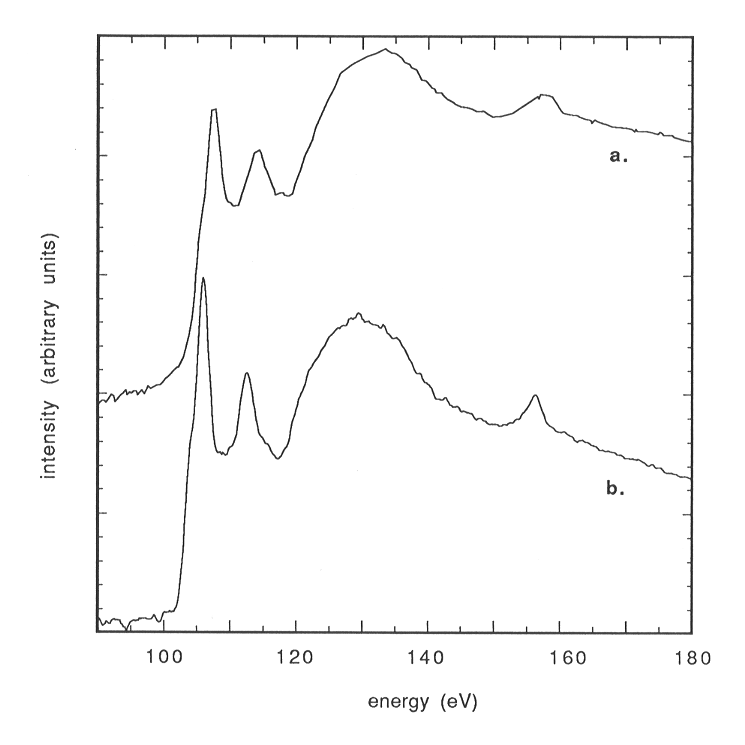This leads to better definition of peaks and shoulders than in the unprocessed spectra (Fig. 3.10-10).
 

Fig. 3.10-10: Si L-edge ELNES spectrum of quartz. a: raw spectrum (exponential background removed). b: Fourier-ratio and zero-loss peak deconvoluted spectrum. Note the improved resolution of the spectrum.

3. Plural scattering can be successfully removed by Fourier-transform-deconvolution of the spectra with the plasmon-peak.

4. The spectra can be further evaluated by subtracting the exponential background and then fitting the edge to a number of Lorentzian lines plus an arctan step function (describing the transition of an electron to the continuum). However, the position of the arctan background is poorly constrained by the spectra, and the detector characteristics can distort the exponential background such that additional fitting parameters have to be taken into account. An example fit of a stishovite Si-K spectrum is shown in Fig. 3.10-11. Optimization of acquisition parameters and processing techniques is improving our resolution and interpretation of the features in ELNES spectra.
 

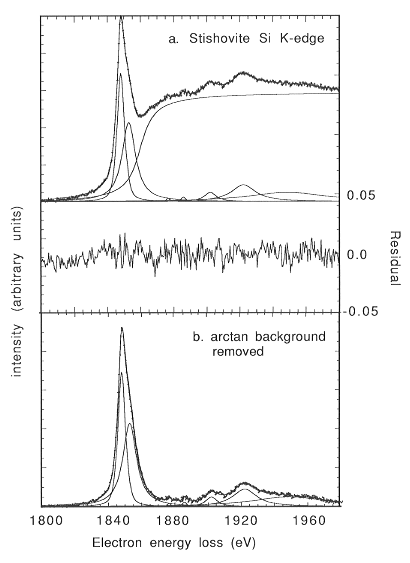Fig. 3.10-11: Si K-edge ELNES spectrum of stishovite. a: raw spectrum (exponential background removed), fitted to 7 Lorentzian lines and an arctan step function. b: arctan background removed. This spectrum is directly comparable to multiple scattering calculations.