

A new approach to parameterize the viscosity-temperature relationships of silicate melts is applied to a data set for 28 aluminosilicate melts based on a haplogranitic chemistry. The approach is based on the introduction of a crossover temperature Tc. Such a crossover temperature has been predicted by the recently developed mode coupling theory (MCT) and neutron and light scattering experiments in simple liquids have demonstrated that a critical temperature Tc can be clearly identified at temperatures above the glass transition temperature (Tg). For simple liquids, this temperature divides a fluid regime with a power-law temperature dependence of viscosity from a viscous regime with a Vogel-Fulcher-Tammann temperature dependence of viscosity. Up to now the question has remained open as to whether MCT can also be applied to strong glass formers (i.e. silicate melts).
A widely discussed classification, based on the temperature dependence of viscosity, was introduced by Angell. Plotting the logarithm of the viscosity (η) as a function of the reduced temperature Tg/T, where Tg is the glass transition temperature (η = 1012 Pa s), the authors obtained curves exhibiting different degrees of non-Arrhenian behaviour. Nearly straight (Arrhenian) lines are observed for highly polymerized network glasses (e.g. SiO2), whereas strong deviations from Arrhenian behaviour are found in particular for systems with non-directional interatomic/intermolecular bonds (e.g. molten salts or simple organic liquids). In a restricted temperature range above Tg the different curves in the η = η(Tg/T) plot are well interpolated by the Vogel-Fulcher-Tammann equation (VFT) η ∝ exp[DT0/(T-T0)], and the parameter D may be considered as a measure of the non-Arrhenian behaviour, i.e. the "fragility". Alternatively a model independent determination of fragility has been introduced by using the slope in plot of log τ versus Tg/T at Tg , where τ is the average relaxation time and Tg the glass transition temperature at τ = 100 s.
Influenced by MCT, Rössler has proposed a scaling procedure in
order to provide a master curve for the temperature dependence of η.
First, log10(η/ηTg)
is plotted as function of (Tg-T)/T where ηTg
is the viscosity at the calorimetric determined glass transition temperature
Tg. Next, the temperature interval (Tc-Tg)/
Tc is scaled to 1 for each glass former. This is accomplished
by multiplying the abscissa with F ≡ Tc
/(Tc-Tg), i.e. log10(η
/η Tg) is plotted versus F(Tg-T)/T.
This procedure is carried out for the reference system o-terphenyl for
which Tc is well known. For all other compositions Tc
is determined by visual inspection in such a way that the viscosity curves
coincide with the curve for o-terphenyl over a temperature range as large
as possible by varying Tc. Fig. 3.7-1 shows the master plot.
The viscosity data of all systems studied over a range of 10 orders of
magnitude, comprising fragile and strong glasses, follow approximately
a master curve. Between Tc and Tg, the non-Arrhenius
character of all curves is quite similar. This implies that parameter D
has an universal value, rather than being a measure of non-Arrhenian behaviour.
In contrast the parameter m, which quantifies the slope of the
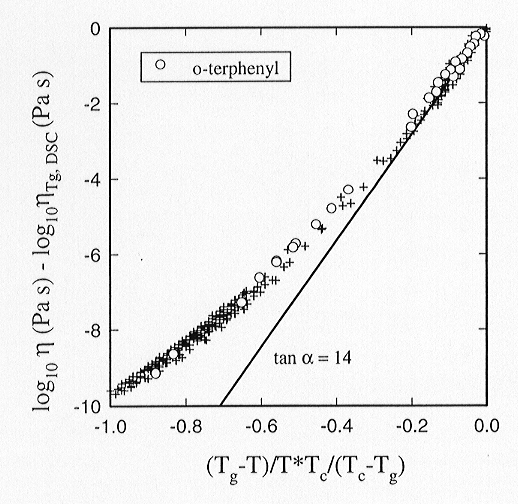 |
Fig. 3.7-1: The master plot. The crosses refer to viscosity data of haplogranitic melt compositions. Tan (α ) ≅ 14 represents the slope of the master curve at Tg. |
relaxation time vs. Tg/T at Tg, can be used. Because the scaling procedure (of the master plot) leads to a master curve very close to Tg , F must be related to m. From the master plot we find that the slope at Tg is about 14 (see straight line in Fig. 3.7-1). Thus we find the relationship: m ≅ 14*F. Introducing the fragility m via the master plot, we obtain improved values for m, and systematic trends appear, when m is now plotted as a function of the melt structure parameter (i.e. NBO/T). In addition Tc can be related to cationic properties such as electronegativity. The success of the master plot raises the possibility that a universal viscosity behaviour exists for all liquids between Tc and Tg and supports the idea that a well-distinguished crossover temperature exists in the melt. Further experiments (e.g. light scattering) will clarify whether Tc as defined by the master plot may be identified with the critical temperature defined in MCT.

Tel: +49-(0) 921 55 3700 / 3766, Fax: +49-(0) 921 55 3769, E-mail: bayerisches.geoinstitut(at)uni-bayreuth.de
 Previous page
Previous page