Previous page     Contents     Next page

The study of the structure of minerals in-situ at high pressures and temperatures is of fundamental importance for developing a proper understanding of the behaviour of such minerals in the interior of the Earth. This is because the macroscopic thermodynamic properties of minerals results from the microscopic (i.e. atomic-level) response of the structure to variables such as pressure and temperature. Single-crystal diffraction at high temperature and/or pressure can provide two important pieces of information about mineral behaviour. First, measurement of the positions of X-ray beams diffracted from the sample enables the unit-cell parameters and volume to be determined, and hence the density to be calculated. The variation of density with depth in the Earth is one of the few parameters that can be obtained with reasonable resolution from seismic data, and the comparison of laboratory data with seismic data places constraints upon possible mineralogies of the mantle. For crustal petrology, the variation of the volume of a mineral with pressure and temperature is one factor that determines the precise pressure and temperature at which reactions occur. Second, measurement of the intensities of diffracted beams from a crystalline sample enable the arrangement of the atoms within a crystal to be determined, thus allowing the development of an understanding of how atomic arrangements effect crystal properties, and in particular how structures respond to applied pressure.

In last year's Annual Report we described the design considerations and installation of a single-crystal diffractometer, built by Huber Diffraktionstechnik GmbH, which was optimised for diffraction from single-crystals held at high pressures in diamond-anvil cells. During 1995 we have developed the orientation and alignment algorithms for this diffractometer, and the software interfaces to drive the diffractometer from both the Vax-VMS and Pentium computers installed in the X-ray laboratory. Initial tests with single crystals in air showed that unit-cell volumes can, in ideal cases, be determined to a precision of about 1 part in 40,000 compared to the precision on a commercial laboratory diffractometer of around 1 part in 5,000 to 10,000. For the last six months, we have been using the diffractometer routinely to measure the volume variation with pressure of a number of crystalline samples. As an example we show in Fig. 3.10-2 the equation of state of an intermediate plagioclase feldspar of composition of An₆₈ determined to a maximum pressure of nearly 6 GPa. The Birch-Murnaghan equation of state fitted to this data yields a room pressure bulk modulus of K_T = 75.4 ± 0.6 GPa and its pressure derivative K´ = 3.4 ± 0.2, with a maximum deviation of the data points from the fitted EOS of 0.025 GPa. This represents an improvement by a factor of approximately 3 in the precision of the EOS parameters over previous diffractometer measurements, and a similar factor in the data point scatter. The scale of this improvement is apparent in Fig. 3.10-2, which also shows data collected on another plagioclase in the author's previous laboratory.
 

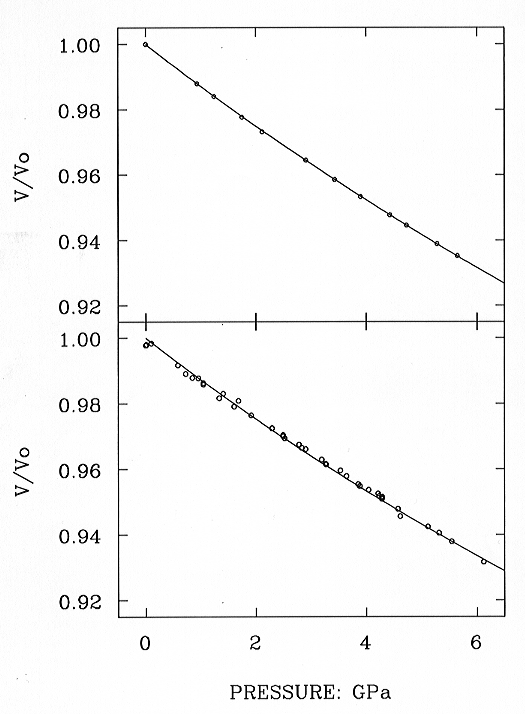Fig. 3.10-2: Top: Equation of state of An68 plagioclase measured on the new four-circle diffractometer. Bottom: Similar measurement of an An100 plagioclase on an older diffractometer, showing increased data scatter.